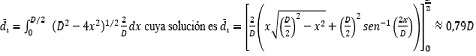La estereología como herramienta matemática se encarga de interpretar imágenes bidimensionales para deducir las estructuras tridimensionales de las que provienen. Así descrita, podría confundirse con la geometría proyectiva o la tomografía, por lo que es necesario añadir un matiz. En estereología, las imágenes bidimensionales analizadas son planos transversales, no necesariamente paralelos entre sí, de la estructura tridimensional objeto de estudio.
Aunque se considera que esta rama de las matemáticas se inicia en el s. XVIII, comienza a desarrollarse a finales del s. XIX y no recibe nombre propio hasta 1961, año en el que se acuña el término “Stereology” y se funda la International Society of Stereology. Esto indica que se trata de una disciplina relativamente reciente y poco conocida, aunque con un gran potencial de aplicación en aquellas ramas de la ciencia que involucran el análisis de secciones microscópicas y macroscópicas, tan dispares como la neurología y la geología.
La relación con la metalografía, el estudio de la estructura interna de los materiales a partir de la observación al microscopio de secciones pulidas de los mismos, es evidente. Por ejemplo, los estándares internacionales de referencia, como el ASTM E112 “Standard Test Methods for Determining Average Grain Size”, emplean la estereología para definir las mismas reglas de medición e interpretación en todo el mundo.
Utilizaremos un caso simple para introducirnos en la aplicación de la estereología en metalurgia, tomando como material de trabajo la fundición de hierro esferoidal ferrítico. La estructura de este material está formada por una matriz de ferrita, en la que existe una dispersión de esferoides de grafito (Figura 1). Las características de esta dispersión, fundamentalmente el número, el tamaño y la forma de estos esferoides, aportan información muy valiosa al metalurgista. A partir de estas características es posible evaluar la corrección de la práctica de fundición y realizar predicciones sobre el comportamiento del material en servicio. Estas evaluaciones se basan en inspecciones de secciones metalográficas.
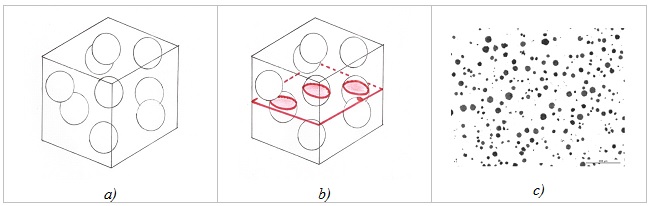
Figura 1. a) Representación de un volumen de fundición nodular; b) Representación de un corte metalográfico (plano en rojo) y la intersección con los grafitos, c) Aspecto de una sección metalográfica real de grafito esferoidal (grafitos en rojo).
Al trabajar sobre superficies metalográficas 2D, no se mide directamente el valor real de los parámetros de interés, sino variables relacionadas con ellos. Plantear gráficamente el problema a mano alzada permite visualizarlo de forma sencilla (Figura 2). Por ejemplo, imagine que necesita medir el diámetro de los grafitos en una muestra. Preparará una superficie metalográfica que cortará de forma aleatoria un número determinado de esferoides, a través de un plano que no coincidirá exactamente con el centro de cada esferoide y, por tanto, los diámetros de grafito observados serán siempre menores que su tamaño real. La distribución de diámetros 2D será nuestra variable que permite predecir, gracias a la estereología, el parámetro que nos interesa: el diámetro medio real de los esferoides.

Figura 2. Ejemplo de tres esferas de grafito de diámetro idéntico D que, al ser cortadas por un mismo plano (recta en rojo) a distintas distancias de su centro, dan lugar a círculos de diámetros d1, d2 y d3.
Como ejercicio introductorio a la estereología, tomaremos un caso ideal en el que todos los grafitos de una hipotética fundición esferoidal sean perfectamente esféricos y tengan todos el mismo diámetro D. Deduciremos la relación entre este diámetro D, que no se puede medir directamente, y los diámetros di medidos al microscopio mediante técnicas metalográficas. Para ello, será necesario aplicar conceptos básicos de geometría, probabilidad y cálculo integral.
Aunque todos los esferoides tengan el mismo diámetro D, los círculos que se observan al microscopio son distintos entre sí. La relación entre el diámetro D y los diámetros di depende de la distancia x al centro de la esfera a la que se practique el corte metalográfico. A través del teorema de Pitágoras (Figura 3): . O escrito de una forma más conveniente.

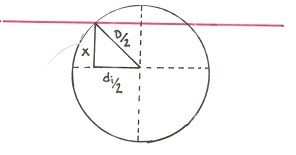
Figura 3. Relación entre la posición del corte x, el diámetro real de la esfera D y el diámetro del círculo di que se observaría sobre la superficie de corte representada por la recta en rojo.
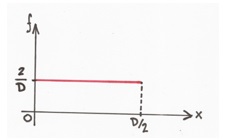
La distancia x puede tomar valores entre 0 y D/2 y todos los planos por los que se puede cortar un grafito son equiprobables. Por tanto, x es una variable aleatoria que sigue una distribución uniforme y su función densidad de probabilidad asociada es f=2/D entre x=0 y x=D/2 (Figura 4).
Figura 4. Función de densidad de probabilidad aplicada en el ejemplo.
El valor medio de los diámetros di se puede obtener combinando las ecuaciones anteriores y recurriendo a la integral
Lo que permite obtener el valor del diámetro real D de las esferas de grafito 3D, en función de la media aritmética de los diámetros di medidos sobre micrografías 2D.
Así, un caso simplificado de análisis estereológico como el recién presentado sobre grafitos esféricos perfectos de diámetro idéntico, puede resolverse en unas pocas líneas, siendo una herramienta fundamental para la actividad metalúrgica de IK4-Azterlan, que a través de avanzadas técnicas de análisis de imagen basadas en la estereología, es capaz de caracterizar de forma rigurosa y precisa muestras que provienen de todo tipo de aleaciones y tecnologías productivas.
Con la esperanza de que en este ejercicio haya sido de su agrado, nos despedimos hasta el próximo post sobre matemáticas para la metalurgia.